Высота звука и частотный спектр

К этому моменту мы уже изучили особенности некоторых свойств звука, а именно тайминг и громкость. Чтобы делать более сложные вещи со звуком, такие как эквализация (например, увеличение низких, басовых частот и уменьшение высоких), нам нужны более сложные инструменты. В этом разделе мы рассмотрим некоторые инструменты, которые позволяют производить более интересные преобразования звука, включая возможность имитировать различные виды сред и манипулировать звуками напрямую с помощью JavaScript.

Основы высоты звука в музыке

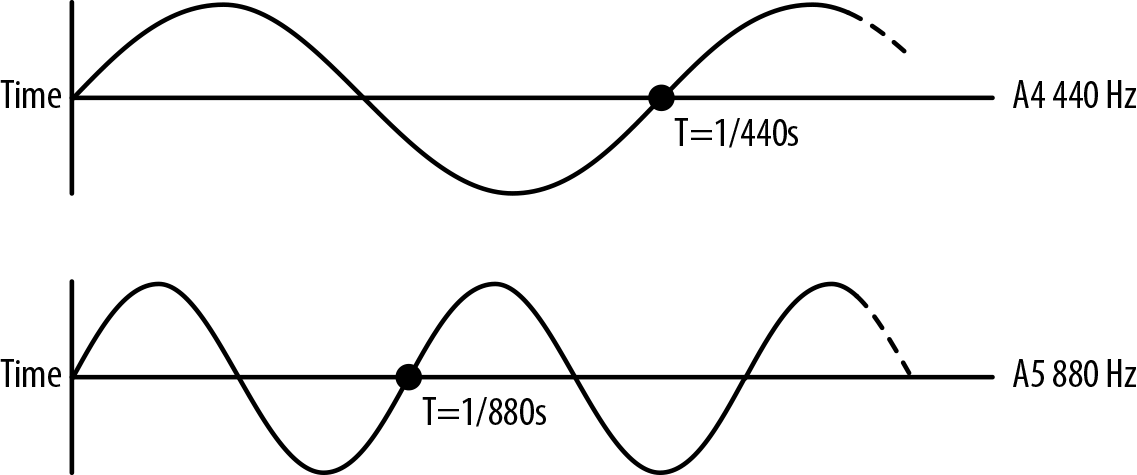
Музыка состоит из множества звуков, воспроизводимых в разное время и одновременно. Звуки, которые извлекаются из музыкальных инструментов, могут быть очень сложными, так как звук отражается от разных частей инструмента и его форма становится уникальной. Однако эти музыкальные тоны имеют одну общую черту: физически они представляют собой периодические волновые формы. Эта периодичность воспринимается нашими ушами как высота звука. Высота измеряется частотой колебаний волны или числом повторений волнового рисунка в секунду, которое указывается в герцах. Частота — это время (в секундах) между гребнями волны. На Рисунке 4-1 видно, что, если мы разделим волну пополам по шкале времени, то получим удвоенную частоту, которая будет звучать как исходный тон, но на одну октаву выше. И наоборот, если уменьшить частоту волны в два раза, тон понизится на октаву. Таким образом, высота звука (как и громкость) воспринимается ушами экспоненциально: на каждой октаве частота удваивается.

Рисунок 4-1. Графики идеальных нот A4 и A5

Октавы разделены на 12 полутонов. Каждая соседняя пара полутонов имеет одинаковое соотношение частот (по крайней мере, в равномерно темперированном строе). Другими словами, соотношение частот A4 к A#4 идентично соотношению частот A#4 к B4.

Рисунок 4-1 показывает то, как можно вывести соотношение между каждым последующим полутоном, учитывая, что:

Для транспонирования ноты на октаву выше, мы удваиваем частоту ноты.
Каждая октава делится на 12 полутонов, которые при равномерно темперированном строе имеют одинаковые соотношения частот.

Пусть f_0 — некоторая частота, а f_1 — эта же частота, но на одну октаву выше. Мы уже знаем отношение между ними:

f_1 = 2 * f_0

Далее, пусть k будет фиксированным множителем между двумя любыми соседними полутонами. Так как всего в октаве 12 полутонов, мы можем вывести следующее:

f_1 = f_0 * k * k * k * ... * k (12x) = f_0 * k^12

Если решить систему этих двух уравнений, получим:

2 * f_0 = f_0 * k^12

Найдём k:

k = 2^(1/12) ~= 1.0595...

К счастью, все эти вычисления смещений, связанных с полутонами, обычно не нужно делать вручную, так как многие аудиосреды (включая Web Audio API) включают в себя понятие расстройки (detune), которое переводит шкалу частот в линейный вид. Расстройка измеряется в центах: каждая октава содержит 1200 центов, а каждый полутон — 100 центов. Указав расстройку в 1200 центов, вы поднимаетесь на октаву выше. Соответственно, расстройка в -1200 центов понижает частоту на октаву.

Высота звука и `playbackRate`

Web Audio API предоставляет параметр playbackRate для каждого узла AudioSourceNode. Это значение можно задать для изменения высоты звука из любого аудиобуфера. Обратите внимание, что в этом случае будут изменены как высота звука, так и длительность семпла. Существуют специальные методы, которые пытаются поменять частоту, не затрагивая длительность семпла, однако довольно сложно сделать это универсальным способом, не внося в микс помех, скретчей и других нежелательных артефактов.

Как мы ранее обсуждали в разделе Основы высоты звука в музыке, для того, чтобы вычислить частоты последовательных полутонов, нужно умножить частоту на соотношение 2^(1/12). Это очень полезно, если вы разрабатываете музыкальный инструмент или используете изменение высоты звука для рандомизации в игровой среде. Следующий код воспроизводит тон с заданным смещением частоты в полутонах:

function playNote(semitones) {
  // Предположим, что новый источник звука был создан из буфера
  var semitoneRatio = Math.pow(2, 1/12);

  source.playbackRate.value = Math.pow(semitoneRatio, semitones);
  source.start(0);
}

Ранее мы обсуждали, что наши уши воспринимают высоту звука экспоненциально. Обрабатывать высоту звука как экспоненциальную величину может быть не очень удобно, поскольку в вычислениях мы постоянно должны использовать такие неудобные значения, как корень двенадцатой степени из двух. Вместо этого мы можем использовать параметр detune, чтобы задать смещение частот в центах. Таким образом можно переписать этот код, используя параметр detune:

function playNote(semitones) {
  // Предположим, что новый источник звука был создан из буфера
  source.detune.value = semitones * 100;
  source.start(0);
}

Если сместить высоту звука на слишком большое количество полутонов (например, вызвав playNote(24)), вы начнёте слышать искажения. Поэтому цифровые пианино включают в себя несколько семплов для каждого инструмента. Хорошие цифровые пианино избегают изменения высоты звука совсем, и включают в себя отдельные семплы для каждой клавиши. Отличные цифровые пианино включают в себя несколько семплов для каждой клавиши, которые воспроизводятся в зависимости от силы нажатия на клавишу.

Множество одновременных звуков с вариациями

Ключевая особенность звуковых эффектов в играх — это то, что их может быть сразу много одновременно. Представьте, что вы в центре перестрелки между множеством игроков, стреляющих друг в друга из пулемётов. Каждый пулемёт стреляет много раз в секунду, вызывая десятки звуковых эффектов, которые должны быть проиграны в один момент. Воспроизведение звуков из множества источников в конкретное и одно и то же время — это то, где Web Audio API по-настоящему отлично себя показывает.

Итак, если все пулемёты в вашей игре звучат абсолютно одинаково, это будет довольно скучно. Конечно же звуки могут варьироваться относительно дистанции до цели и позиции слушателя к другим игрокам (см. Пространственный звук), но даже этого может быть недостаточно. К счастью, Web Audio API предоставляет способ легко модифицировать данный пример как минимум двумя простыми способами:

Добавив небольшой сдвиг по времени между выстрелами.
Изменив высоту звука для лучшей имитации случайности реального мира.

Используя наши знания о тайминге и высоте звука, мы можем легко реализовать эти два эффекта:

function shootRound(numberOfRounds, timeBetweenRounds) {
  var time = context.currentTime;

  // Создаём несколько источников аудио из одного и того же буфера
  // и проигрываем в быстрой последовательности
  for (var i = 0; i < numberOfRounds; i++) {
    var source = this.makeSource(bulletBuffer);

    source.playbackRate.value = 1 + Math.random() * RANDOM_PLAYBACK;
    source.start(time + i * timeBetweenRounds + Math.random() * RANDOM_VOLUME);
  }
}

Web Audio API автоматически объединяет несколько звуков, воспроизводимых одновременно, по сути просто складывая формы волн. Это может привести к таким проблемам, как клиппинг, о котором мы говорили ранее в разделе Клиппинг и измерения уровня сигнала.

Этот пример добавляет некоторую вариативность к узлам AudioBuffer, которые мы загрузили из звуковых файлов. В некоторых случаях желательно использовать полностью синтезированные звуки и не пользоваться буферами в принципе (см. Процедурно сгенерированный звук).

Понятие частотного спектра

До этого момента в наших теоретических упражнениях мы рассматривали звук как функцию давления, меняющегося со временем. Однако есть и другой полезный способ анализа звука — отобразить амплитуду и посмотреть, как она меняется в зависимости от частоты. В итоге мы получим графики, в которых область определения функции (ось X) выражается в единицах частоты (Hz). Такие графики описывают звук в частотном спектре.

Связь между графиками во временном и частотном спектрах основана на идее разложения Фурье. Как мы уже видели, звуковые волны часто имеют циклическую природу. Математически периодические звуковые волны можно рассматривать как сумму нескольких простых синусоид разных частот и амплитуд. Чем больше таких синусоид мы складываем, тем точнее получается приближение исходной функции. Мы можем взять сигнал и выделить его составляющие синусоиды, применив преобразование Фурье. Для такого разложения существует множество алгоритмов, самый известный из них – быстрое преобразование Фурье (FFT). К счастью, в Web Audio API уже встроена реализация этого алгоритма. Далее мы рассмотрим, как это устроено (см. Частотный анализ).

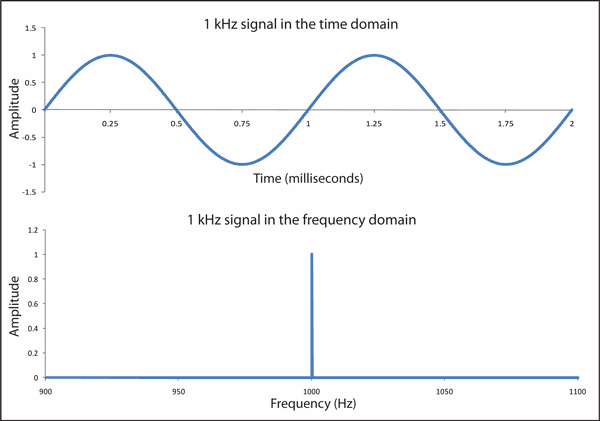
В общем случае мы можем взять звуковую волну, вычислить составляющую её синусоиду и нанести в виде точек (частоту, амплитуду) на график, чтобы получить график частотного спектра. На Рисунке 4-2 показана чистая нота ля (A) на частоте 440 Hz (A4).

Рисунок 4-2. Идеальная синусоидальная волна 1 кГц, представленная в частотном и временном спектрах

Анализ графика частотного спектра может дать лучшее представление о качествах звука, таких как высота тона, содержание шума в спектре и многих других. На основе частотного спектра можно построить продвинутые алгоритмы, такие как определение высоты тона. У звука, который произведён реальными музыкальными инструментами есть обертоны, так что нота A4, сыгранная на пианино, будет иметь график частотного спектра, который сильно отличается от графика той же ноты A4, но сыгранной на трубе. Независимо от сложности звуков, здесь будут также применимы идеи разложения Фурье. На Рисунке 4-3 показан более сложный фрагмент звука как во временном, так и в частотном спектре.

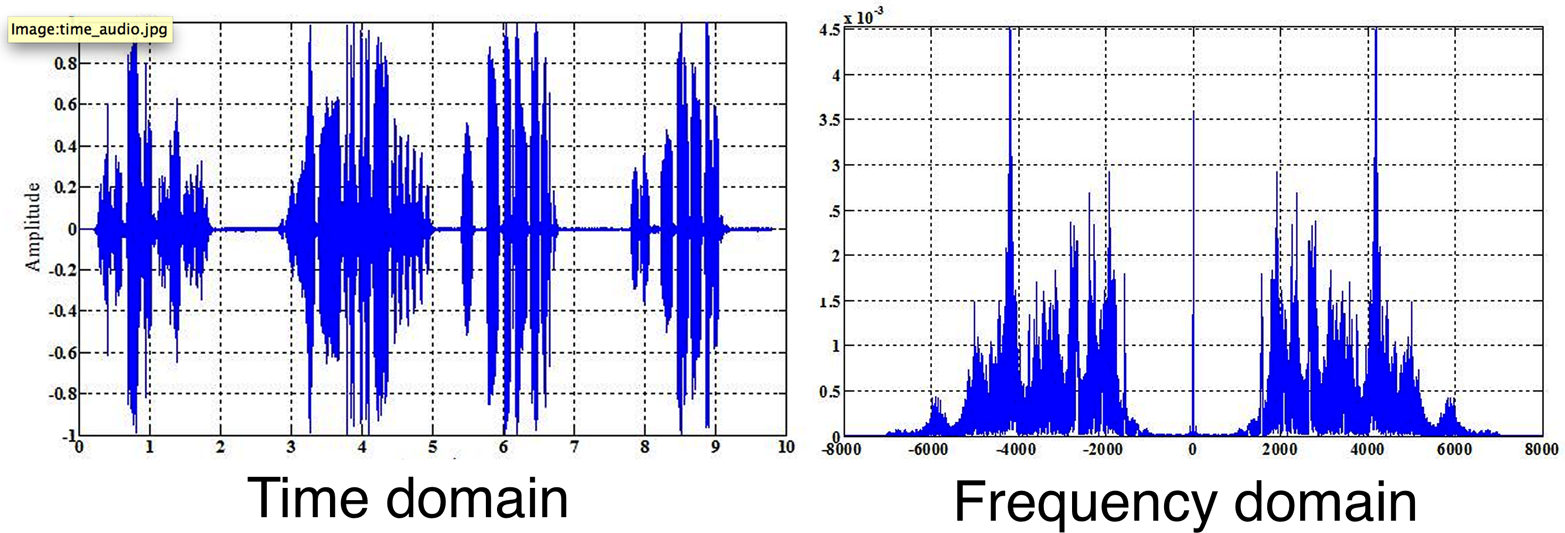
Рисунок 4-3. Сложный звуковой сигнал, представленный в частотном и временном спектрах

Эти графики ведут себя довольно по-разному с течением времени. Если бы вы очень медленно проигрывали звук, который изображён на Рисунке 4-3 и наблюдали бы изменение обоих графиков, вы бы заметили, что график временного спектра (слева) продвигается слева направо. График частотного спектра (справа) — это результат анализа звуковой волны в определённый момент времени, поэтому он мог бы меняться намного быстрее и куда менее предсказуемо.

Важно отметить, что частотный анализ по-прежнему полезен, даже когда исследуемый звук не воспринимается как имеющий определённую высоту. Звуки ветра, ударов и выстрелов имеют характерный вид на графике частотного спектра. Например, белый шум имеет плоский спектр в частотной области, так как все частоты в нём представлены одинаково.

Прямой синтез звука на основе осциллятора

Ранее мы обсуждали, что цифровой звук в Web Audio API представлен в виде массива чисел в узлах AudioBuffer. В большинстве случаев, буфер создаётся при загрузке звукового файла или на лету из какого-то звукового потока. Но иногда нам может понадобиться синтезировать собственные звуки. Мы можем сделать это, программно создав аудиобуферы через JavaScript, просто вычисляя математическую функцию через равные промежутки времени и записывая значения в массив. Такой подход позволяет вручную изменять амплитуду и частоту синусоиды или даже объединять несколько синусоид, чтобы создавать произвольные звуки (вспоминаем преобразования Фурье из раздела Понятие частотного спектра).

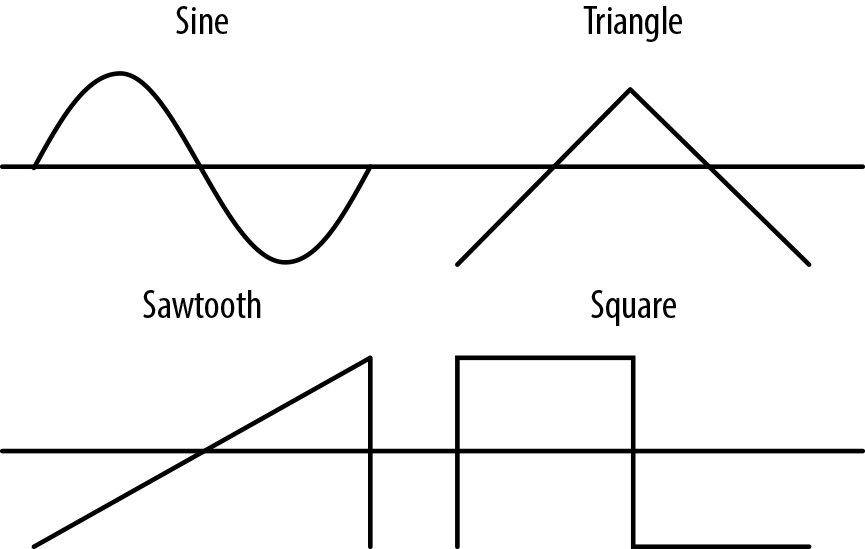
Хоть это и реализуемо, но разработка такого функционала на JavaScript будет сложной и неэффективной. Вместо этого Web Audio API предоставляет примитивы, которые позволяют делать то же самое при помощи узлов осцилляторов OscillatorNode. Эти узлы имеют настраиваемые параметры частоты и расстройки (см. Основы высоты звука в музыке). Также можно задать тип генерируемой волны. Встроенные типы включают синусоидальную, треугольную, пилообразную и прямоугольную волны, как показано на Рисунке 4-4.

Рисунок 4-4. Базовые типы волн, которые может генерировать осциллятор

Осцилляторы могут быть легко использованы в аудиографах вместо узлов AudioBufferSourceNode. Посмотрим на пример ниже:

function play(semitone) {
  // Создадим необходимые узлы
  var oscillator = context.createOscillator();
  oscillator.connect(context.destination);

  // Проиграем синусоидальную волну на частоте в 440 Hz (A4)
  oscillator.frequency.value = 440;
  oscillator.detune.value = semitone * 100;

  // Обратите внимание, что эта константа будет заменена на "sine"
  oscillator.type = oscillator.SINE;
  oscillator.start(0);
}